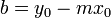yasmin: matematica

IDENTIDADES TRIGONOMETRICAS

las identidades trigonométricas verificables para cualquier valor permisible de la variable o variables que se consideren (es decir, para cualquier valor que pudieran tomar los ángulos sobre los que se aplican las funciones).
Estas identidades, son útiles siempre que se precise simplificar expresiones que incluyen funciones trigonométricas. Otra aplicación importante es el cálculo de integrales indefinidas de funciones no-trigonométricas: se suele usar una regla de sustitución con una función trigonométrica, y se simplifica entonces la integral resultante usando identidades trigonométricas.
Notación: se define cos²α, sen²α, etc; tales que sen²α es (sen α)².

trigonométricas

$\tan{x} = \frac {\operatorname{sen}{x}} {\cos{x}} \qquad \cot{x} = \frac{1} {\tan{x}} = \frac{\cos{x}}{\operatorname{sen}{x}}$

$\sec{x} = \frac{1} {\cos{x}} \qquad \csc{x}= \frac{1}{\operatorname{sen}{x}}$

Son más sencillas de probar en la circunferencia trigonométrica o goniométrica (que tiene radio igual a 1):

$\operatorname{sen}(x) = \operatorname{sen}(x + 2\pi) \qquad \cos(x) = \cos(x + 2\pi) \qquad \tan(x) = \tan(x + \pi)$

$\operatorname{sen}(-x) = \operatorname{sen}(x+\pi) \qquad \cos(-x) = -\cos(x+ \pi)$

$\tan(-x) = -\tan(x) \qquad \cot(-x) = -\cot(x)$

$\operatorname{sen}(x) = \cos\left(\frac{\pi}{2} - x\right) \qquad \cos(x) = \operatorname{sen}\left(\frac{\pi}{2}-x\right) \qquad \tan(x) = \cot\left(\frac{\pi}{2} - x\right)$

El plano cartesiano es un sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas (o rectangulares) x e y se denominan abscisa y ordenada, respectivamente.